Question

This might be a tough question to understand and answer but I need help. So can you tell whether the ordered pair (-2,-2) is a solution of the system of linear equations? And can you solve the system of linear equations by graphing?

Answer 1

Answer:

(-2, -2) is not a solution of the system of linear equations.

The graph is shown below:

The solution is (x, y) = (3, 1)

Step-by-step explanation:

Given the system of equations below:

`\begin{gathered} y=-(1)/(3)x+2 \\ \\ y=x-2 \end{gathered}`

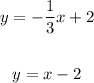
Suppose (-2, -2) satisfy these equations, then substitution x = -2, and y = -2 in each equation makes the left-hand side equal to the righ-hand side.

For the first equation:

`\begin{gathered} -2=-(1)/(3)(-2)+2 \\ \\ -2=(8)/(3) \\ \\ \text{But} \\ -2\\e(8)/(3) \end{gathered}`

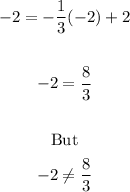
Therefore, this is sufficient to say that (-2, -2) is not a solution of the system of linear equations