Question

Factorise :
`12x ^(2) - 7x + 1`hey can you please help me solve this

Answer 1

(4x-1)(3x-1)

Explanation:

Given the quadratic expression:

`12x^2-7x+1`

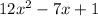
To factorize, follow the steps below.

Step 1: Multiply the coefficient of x² and the constant.

`12*1=12`

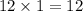
Step 2: Find two numbers that multiply to give 12, and add to give the coefficient of x, -7.

• To do this, list the factors of 12: 1,2,3,4,6,12

,

• Then select your two numbers by observation.

`\begin{gathered} 4*3=12 \\ -4-3=-7 \end{gathered}`

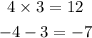
Step 3: Rewrite the middle with those numbers.

`12x^2-7x+1=12x^2-4x-3x+1`

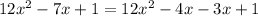
Step 4: Factor the first two and last two terms separately.

Ensure that the expression in the brackets is the same.

`\begin{gathered} =4x(3x-1)-1(3x-1) \\ =(4x-1)(3x-1) \end{gathered}`

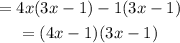
The factored form is (4x-1)(3x-1).