Question

A 0.05 kg tennis ball moves at a speed of 10 m/s and is struck by a racket causing it to rebound in the opposite direction at a speed 16 m/s. What is the change in momentum of the ball? What is the impulse exerted on the ball? What is the impulse exerted on the racket?

Answer 1

Δp = -1.3 kg m/s

Impulse on the ball = Δp = -1.3 kg m/s

Impulse on the racket = 1.3 kg m/s

Step-by-step explanation:

The change in momentum of the ball can be calculated as

`\Delta p=mv_f-mv_i`

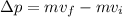
Where m is the mass of the tennis ball of 0.05 kg, vf is the final velocity and vi is the initial velocity. Since the ball rebound in the opposite direction, we will replace vf = -16 m/s and vi = 10 m/s

Replacing the values, we get

`\begin{gathered} \Delta p=0.05\text{ kg\lparen-16 m/s\rparen-0.05 kg\lparen10 m/s\rparen} \\ \Delta p=-0.8\text{ kg m/s - 0.5 kg m/s} \\ \Delta p=-1.3\text{ kg m/s} \end{gathered}`

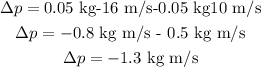
Therefore, the change in momentum of the ball is -1.3 kg m/s.

Then, the impulse exerted on the ball is equal to the change in momentum, so

Impulse on the ball = Δp = -1.3 kg m/s

Finally, the impulse exerted on the racket is equal to the impulse of the ball but with the opposite sign, so

Impulse on the racket = 1.3 kg m/s