Since they are similar triangles, then it is true that
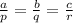
So, in this case, you have
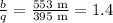
Then
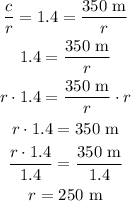
On the other hand,

Finally, finding the perimeter of the triangular track, that is, adding the sides
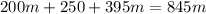
Therefore, If Chang jogs one lap around the inside track, he runs 845 meters and the correct answer is B. 845 m.