Question

an airplane travels 2212 kilometers against the wind in 4 hours and 2732 kilometers with the wind in the same amount of time. what is the rate of the plane in still air and what is the rate of the wind?

Answer 1

We are told that the airplane traveled 2212km against the wind(the wind was resisting it) in 4 hours, this can be expressed mathematically as below;

`\begin{gathered} p-w=(2212)/(4) \\ p-w=553 \end{gathered}`

where p = rate of the plane in still air in km/h

w = rate of the wind in km/h

We're also told that plane later traveled 2732km with the wind( so the wind was assisting it), so the relative speed here can be expressed as;

`\begin{gathered} p+w=(2732)/(4) \\ p+w=683 \end{gathered}`

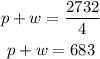
So we now have 2 equations, let's go ahead and solve them simultaneously by adding p-w = 553 to p+w = 683;

`\begin{gathered} 2p=1236 \\ p=(1236)/(2) \\ \therefore p=618 \end{gathered}`

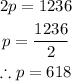
Therefore the rate of the plane in still air is 618kmph.

To find the rate of the wind, let's use the 2nd equation and substitute p = 618;