Question

.An automobile accelerates uniformly from 0 to 24 m/s in 6.0 s. If the car has a massof 2.0x10^3kg, what is the force accelerating it?

Answer 1

8000 Newtons

Step 1

find the acceleration

the acceleration can be calculated by using the formula:

`a=(\Delta velocity)/(\Delta time)=\frac{v_f-v_1}{\text{time taken}}`

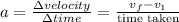
then,let

`\begin{gathered} v_i=0 \\ v_f=\text{ 24}(m)/(s) \\ \text{time}=\text{ 6 sec} \end{gathered}`

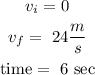
now, replace in the formula

`\begin{gathered} a=(\Delta velocity)/(\Delta time)=\frac{v_f-v_1}{\text{time taken}} \\ a=\frac{24(m)/(s)-0(m)/(s)}{6\text{ s}} \\ a=4(m)/(s^2) \end{gathered}`

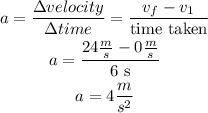
Step 2

find the force.

Newton's Second Law of Motion says that acceleration happens when a force acts on a mass (object), it is given by:

`\begin{gathered} F=\text{ ma} \\ \text{where m is the mass} \\ \text{and a is the acceleration} \end{gathered}`

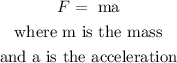
then, let

now, replace

therefore , the answer is

8000 Newtons

I hope this helps you