Question

In the diagram shown below, triangle JKN ~ triangle NKM ~ triangle MKL.What is the length, in units, of NM? Show your work. Explain your reasoning.thank you ! :)

Answer 1

`NM=2√(3)\text{ }units`

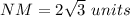
Step-by-step explanation:

We are given that the 3 triangles are similar. This means that the corresponding angles of each triangle are equal.

We are given the measure of the angle NMK = 60º. Since the triangle NKM is similar to triangle MKL, the angle MLK = 60º = NMK

We have the triangle MKL:

Now, we can use the trigonometric ratio sine, to find the length of MK:

`\sin(60º)=(MK)/(8)`

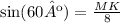
Thus:

`MK=8\sin(60º)=8\cdot(√(3))/(2)=4√(3)`

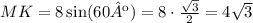
And now, if we look at the triangle NKM:

And now, we can find the asked length, the length of side NM.

Using the trigonometric ratio cosine:

`\cos(60º)=(NM)/(4√(3))`

And solve:

`NM=4√(3)\cos(60º)=4√(3)\cdot(1)/(2)=2√(3)`

Thus, the length of side NM is 4√3