Since we want to create groups of 3 students among 20 possible spots, and the order of the elements (students) inside each group of 3 is important (the order of students change the group and the photograph), we have a permutation problem.
The formula to calculate a permutation of n choose p is:
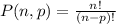
For this problem, let's use n = 20 and p = 3, so we have:
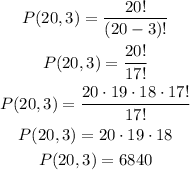
So there are 6840 different ways the 3 students can sit in the chairs.