The vertex of the quadratic is (-3,-5) and the y intercept is (0,13).
The general form of the quadratic is,

Substituting the value of (0,13),
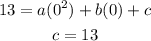
The vertex is at point (-3,-5),
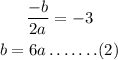
Also (-3,-5) satisfies the equation,
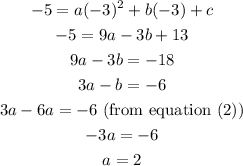
from equation (2),
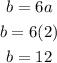
Thus, the quadratic can be formed by substituting the values of a, b and c,
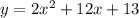
Thus, option (A) is correct.