Question

Question 4 (Essay Worth 10 points)(01.07 MC)The dimensions of a rectangular prism are shown below:Length: 11 feet12.Width: 1 foot122The lengths of the sides of a small cube are foot each2Part A: How many small cubes can be packed in the rectangular prism? Show your work. (5

Answer 1

We will investigate composite bodies of various types.

We have a rectangular prism with the following dimensions:

`\begin{gathered} \text{Length ( L ) = 1}(1)/(2)\text{ = 1.5 ft} \\ \\ \text{Width ( w ) = 1 foot} \\ \\ \text{Height ( h ) = 2}(1)/(2)\text{ = 2.5 ft} \end{gathered}`

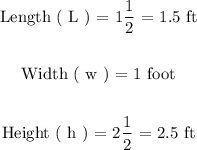
We are to fill an empty rectangular prism with ( n ) number of small cubes with dimension as follows:

`\text{Side length ( a ) = }(1)/(2)ft\text{ = 0.5 ft}`

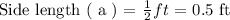
We will determine the volume occupied by ( n ) number of cubes. The general formula for the volume of a cube is as follows:

`\text{Volume ( cube ) = a}^3`

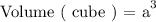
Then for ( n ) number of cubes the volume occupied is:

`\begin{gathered} \text{Volume ( n cubes ) = n}\cdot a^3 \\ \text{Volume ( n cubes ) = n}\cdot0.5^3 \\ \\ \text{Volume ( n cubes ) = n}\cdot(1)/(8)ft^3 \end{gathered}`

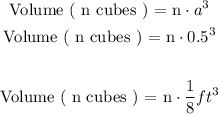
The volume of an empty rectangular prism is defined as follows:

`\text{Volume ( rectangular prism ) = L}\cdot w\cdot h`

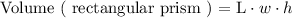
Using the given dimensions we can compute the volume of the prism as follows:

`\begin{gathered} \text{Volume ( rectangular prism ) = ( 1.5 ) }\cdot\text{ ( 1 ) }\cdot\text{ ( 2.5 )} \\ Volume(rectangularprism)=3.75ft^3\text{ } \\ \end{gathered}`

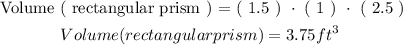
The ( n ) number of small cubes must occupy the entire volume of the rectangular prism. So we will go ahead and equate the volumes of each as follows:

`\text{Volume ( rectangular prism ) = Volume ( n cubes )}`

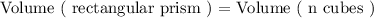
Plug in the respective expressions and solve for the variable ( n ) as follows:

`\begin{gathered} n\cdot(1)/(8)\text{ = 3.75} \\ \\ n\text{ = 30 cubes} \end{gathered}`

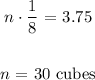
Therefore, we can pack 30 cubes into the rectangular prism!