Given:
Mean=21.
Standard deviation, SD=3.
The percentage of cars sold between 18 and 24 days is to be found.
So, upper value=24.
Lower value=18
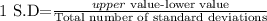
Now, find total number of standarde deviations from above equation.

A total of two standard deviations implies that there is one standard deviation on either side of the mean.
Generally, 68% of the values are within one standard deviation of the mean.
Hence, option C is correct.