Question

Find x and y in each of these following figures

Answer 1

For any given right angled triangle, we can solve for unknown sides and angles using trig ratios sine, cosine and tangent.

Note that the reference angle would be given and then the side facing the reference angle is the OPPOSITE. The side facing the 90 degree angle is the HYPOTENUSE, and the third side, between the reference angle and the 90 degree angle is the ADJACENT.

Looking at triangle number 17, the sides are;

`\begin{gathered} U\sin g\text{ angle 30}\degree\text{ as the reference angle,} \\ \text{Opposite}=6 \\ \text{Hypotenuse}=x \\ \text{Adjacent}=y \end{gathered}`

To calculate side x, note that we have side 6 already which means we have the OPPOSITE and the HYPOTENUSE. We can now use the trig ratio;

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin 30=(6)/(x) \end{gathered}`

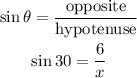
We shall now take note of the given values of special angles 30, 45 and 60 degrees.

Note the following;

`\sin 30=(1)/(2)`

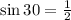
Substitute for this into the equation and we now have;

`\begin{gathered} \sin 30=(6)/(x) \\ (1)/(2)=(6)/(x) \\ \text{Cross multiply and you'll have;} \\ x=(6*2)/(1) \\ x=12 \end{gathered}`

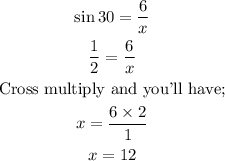
To calculate side length y, note that side y is the ADJACENT, (using 30 degrees as the reference angle).

Taking the adjacent and the HYPOTENUSE (side length x = 12), we would now have;

`\begin{gathered} \cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \cos 30=(y)/(12) \\ \end{gathered}`

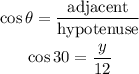
Take note of the following;

`\cos 30=\frac{\sqrt[]{3}}{2}`

We substitute this and we have;

`\begin{gathered} \cos 30=(y)/(12) \\ \frac{\sqrt[]{3}}{2}=(y)/(12) \\ \text{Cross multiply and we'll have;} \\ \frac{12\sqrt[]{3}}{2}=y \\ 6\sqrt[]{3}=y \end{gathered}`

Therefore;

ANSWER: (17)

`x=12,y=6\sqrt[]{3}`