Let's check every way:
* Multiply 4p + 2q = 62 by 2, then subtract 8p - q = 59 from the result:

The first way works really well since we are able to eliminate one of the variables and get one equation and one unknown, which is very simple to solve.
-------------------------------
Multiply 8p - q = 59 by 2, then add the result to 4p + 2q = 62:
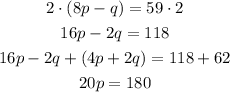
The second way is also a valid option since we were able to eliminate one of the variables ang get a equation with one unknown.
------------------------------------------
Both methods work really well, in the first method we eliminated the variable p and in the second method we eliminated the variable q.