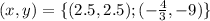Given the system of equations:
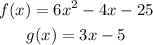
To solve the system of equations, we will solve the following equation:
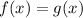
so,
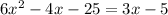
Solve the quadratic equation as follows:
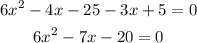
The last equation will be solved using the general formula:
a = 6, b = -7, c = -20
![\begin{gathered} x=\frac{7\pm\sqrt[]{(-7)^2-4\cdot6\cdot(-20)}}{2\cdot6}=(7\pm23)/(12) \\ \\ x=(7+23)/(12)=2.5 \\ or \\ x=(7-23)/(12)=-(4)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/z1pum4guj6km49u00j07fiij3mggme49ag.png)
So, there are two points of intersection for the given system
For each value of (x) substitute into g(x) to find the value of (y)
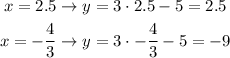
So, the answer will be, the point of intersections are: