Question

a major Fishing Company does its fishing in a local Lake. the first year of the company's operation it managed to catch 170000 fish due to population decreases the number of fish the company was able to catch decreased by 8% each year how many total fish did the company catch over the first 8 years. use sum finite geometric series formula to solve

Answer 1

The number of Fishes caught by the company over the first 8 years is 1,034,410 fishes

Here, we want to find the sum of the fishes the company was able to catch over the first 8 years

We start by setting up an exponential equation to represent the number of fishes caught at any number of years in time

We can have the exponential equation as;

`P(t)=I(1-r)^(t-1)`

where I is the population of fishes in the first year

r is the percentage decrease which is 8% and it is same as 8/100 = 0.08

t is the year number

and P(t) is the population at a certain year

So substituting these values, we have;

`\begin{gathered} P(t)=170,000(1-0.08)^(t-1) \\ \\ P(t)=170,000(0.92)^(t-1) \end{gathered}`

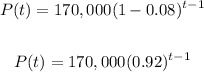
So in this case, we have a geometric series with the nth term given above such that;

The first term a, is 170,000

The common ratio is 0.92

So the sum of the first 8 years which is the sum of the first 8 terms can be obtained using the formula for the geometric series as follows;

`\begin{gathered} S_n\text{ = }(a(1-r^n))/(1-r) \\ \\ S_8\text{ = }\frac{170,000(1-0.92^8)}{1-\text{ 0.92}} \\ \\ S_8\text{ =}(170,000(0.48678))/(0.08) \\ \\ S_8\text{ = }(82,752.792)/(0.08) \\ \\ S_8\text{ = 1,034,409.89} \\ \\ To\text{ the nearest integer, this is 1,034,410} \end{gathered}`