Question

If 40 = 62° and side x = 5, find the length of sides y and r.

Answer 1

STEP 1: Identify and Set Up

We are given a right angled triangle with an acute angle and the length of the line adjacent to it. With this data, we can get a number of other variables including the length of the line opposite the angle (y) and the hypothenuse (r). We will frequently employ the SOH CAH TOA mnemonic to do so.

STEP 2: Execute

`\cos \theta=(adjacent)/(hypothenuse)\text The CAH is employed. Look at the 1st letters`
`\begin{gathered} \cos 62=(x)/(r)=(5)/(r) \\ To\text{ find r, we multiply both sides by r and divide by cos62 to get:} \\ r=(5)/(\cos 62)=10.65 \end{gathered}`

To find our other variable, y we employ another identity.

`\tan \theta=\frac{\text{opposite}}{\text{adjacent}}\text Look at the first letters`
`\begin{gathered} \tan 62=(y)/(x)=(y)/(5)\text Observe that y is the line opposite \theta \\ To\text{ get y, we multiply both sides by 5} \\ y=5\tan 62=9.40 \end{gathered}`

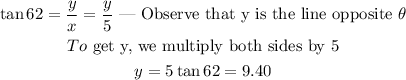
y = 9.40 and r = 10.65 (OPTION D)