Given:
Rate of decrease each minute = 1.7% = 0.017
Let's solve for the following:
• (a). Given:
Initial temperature = 190 degrees
Let's find the temperature after 20 minutes.
Apply the exponential decay formula:
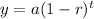
Where:
t is the time in minutes = 20 mins
a is the initial temperature = 190 degrees
r is the decay rate = 0.017
The equation below represents this situation:
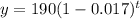
Plug in values into the formula and solve for y.
We have:
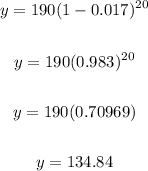
Therefore, the temperature after 20 minutes will be:
134.84 degrees Fahrenheit.
• (b). How long after you place the chicken breast in the freezer will it be frozen?
We have the graph below:
The chicken will get frozen when the temperature gets to 0 degrees.
From the graph, it will get frozen at 750 minutes
ANSWER:
• (a). 134.84 degrees Fahrenheit
,
• (b). 750 minutes.