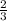Given:
The coordinates of a triangle MSV are, M(-3,3), S(6,3), and V(3, -3).
The coordinates of a triangle M'S'V' are, M'(-2,2), S'(4,2), and V'(2, -2).
To find the scale factor:
Using the scale factor formula,
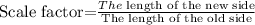
The length of the new side M'S' is
![\begin{gathered} M^(\prime)S^(\prime)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(4-(-2))^2+(2-2)^2} \\ =\sqrt[]{(4+2)^2+0} \\ =\sqrt[]{6^2} \\ =6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lpq8p9wfxi0isvaix5ukgsz4ijgjcjoe2k.png)
The length of the old side MS is
![\begin{gathered} MS=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(6-(-3))^2+(3-3)^2} \\ =\sqrt[]{(6+3)^2+0} \\ =\sqrt[]{9^2} \\ =9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xtocfwaape7u8ujs3w3iql8rnvfpnbfdb0.png)
Then, the scale factor is,
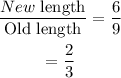
Hence, the scale factor is,