Question

HELP, I NEED SOMEBODY

2.Solve the equation p^2 + 4p = 1 by completing the square. Show your work

Answer 1

The given equation is

`p^2+4p=1`

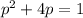
To use the completing square, divide 4p by 2 to find the product of the 2 terms of the bracket

`(4p)/(2)=2p`

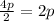
Since 2p = 2 x p, then the bracket is (p + 2)

Let us make it power 2 and state its terms

`\begin{gathered} (p+2)^2=(p)(p)+(p)(2)+(2)(p)+(2)(2) \\ (p+2)^2=p^2+2p+2p+4 \\ (p+2)^2=p^2+4p+4 \end{gathered}`

We have already p^2 and 4p, then we must add 4, then

Add 4 to both sides of the equation

`\begin{gathered} p^2+4p+4=1+4 \\ (p+2)^2=5 \end{gathered}`

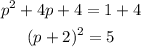
Now, let us take the square root to both sides

`\begin{gathered} \sqrt[]{(p+2)^2}=\pm\sqrt[]{5} \\ p+2=\pm\sqrt[]{5} \end{gathered}`

Subtract 2 from both sides

`\begin{gathered} p+2-2=\pm\sqrt[]{5}-2 \\ p=\pm\sqrt[]{5}-2 \end{gathered}`

The solutions of the equation are

`p=\sqrt[]{5}-2,p=-\sqrt[]{5}-2`