Answer:
274.8 feet
Step-by-step explanation:
The diagram illustrating this problem is attached below:
The distance between the boat and the bottom of the lighthouse = x
Using trigonometric ratio:
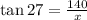
Cross multiply:
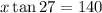
Divide both sides by tan 27.
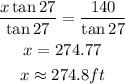
The horizontal distance between the boat and the bottom of the light house is 274.8 feet (correct to the nearest tenth)