Question

If this makes any sense to you please help me and explain?

Answer 1

Given:

The demand function is

`p=-(1)/(20)x+920`

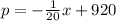
The cost function is

`C(x)=80x+6000`

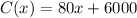
a)

Required:

We need to find the revenue function.

Step-by-step explanation:

Multiply the demand function by x to find the revenue function.

`R(x)=xp`
`Substitute\text{ }p=(-1)/(20)x+920\text{ in the equation.}`
`R(x)=x((-1)/(20)x+920)`
`R(x)=(-1)/(20)x^2+920x`

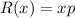
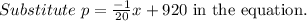
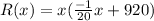
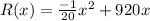
Answer:

`R(x)=-(1)/(20)x^2+920x`

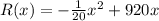
b)

Required:

We need to find the profit.

Step-by-step explanation:

Recall that Profit=Revenue -Cost.

`P(x)=R(x)-C(x)`
`Substitute\text{ }R(x)=(-1)/(20)x^2+920x\text{ and }C(x)=80x+6000\text{ in the equation.}`

`P(x)=(-1)/(20)x^2+920x\text{ -\lparen}80x+6000)`
`P(x)=(-1)/(20)x^2+920x-80x-6000`
`P(x)=(-1)/(20)x^2+840x-6000`

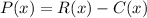
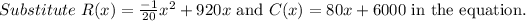
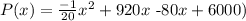
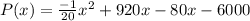
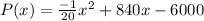
Answer:

`P(x)=(-1)/(20)x^2+840x-6000`

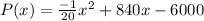
c)

Required:

We need to find the maximum profit.

Step-by-step explanation:

Consider the profit function.

`P(x)=(-1)/(20)x^2+840x-6000`

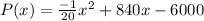
Differentiate this function with respect to x.

`P^(\prime)(x)=(-1)/(20)(2x)+840(1)-6000(0)`
`P^(\prime)(x)=(-1)/(10)x+840`

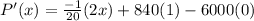
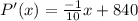
Set P'(x) =0 to find the value of x that maximizes profit.

`(-1)/(10)x+840=0`

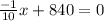
Subtract 840 from both sides.

`(-1)/(10)x+840-840=0-840`
`(-1)/(10)x=-840`

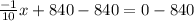
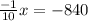
Multiply both sides by (-10).

`(-1)/(10)x(-10)=-840(-10)`
`x=8400`

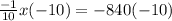
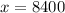
Substitute x =8400 in the profit function to find the maximum profit.

`P(8400)=(-1)/(20)(8400)^2+840(8400)-6000`
`P(8400)=3522000`

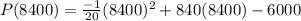
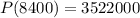
Answer:

The value of x that maximizes profit is 8400.

The maximum profit is $3,522,000.

d)

Required:

We need to find the price charged to maximize the profit.

Step-by-step explanation:

Substitute x =8400 in the demand function.

`p=-(1)/(20)(8400)+920`
`p=500`

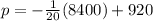
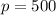
Answer:

The price charged to maximize the profit is $500.