Answer:
The slopes are the same and the y-intercepts are different.
Step-by-step explanation:
Given:
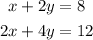
Recall that the slope-intercept equation of a line is generally given as;

where;
m = slope of the line
b = y-intercept of the line
Let's go ahead and rewrite the first equation in slope-intercept form as seen below;
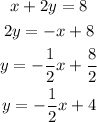
We can see from the above that the slope(m) of the first equation is -1/2 and the y-intercept(b) is 4.
Let's go ahead and rewrite the second equation in slope-intercept form as seen below;
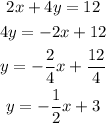
We can see from the above that the slope(m) of the second equation is -1/2 and the y-intercept(b) is 3.
We can see from the above that, for the two equations, the slopes are the same, and the y-intercepts are different.