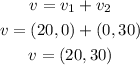Part A.
30 miles east in half hour next
turn left and drive 30 miles north in 1 hour
The average speed is given by
the total distance divided by the total amount of time.
In this case,

Now, the position in rectangular coordinates is (30,30)
In polar coordinates, we must find the angle theta and the lenght r.
This can be given as
![\begin{gathered} r=\sqrt[]{x^2+y^2} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h52e8zdh834uarsbbzgay55udia1e357ww.png)
In our case x=30 and y=30, hence
![\begin{gathered} r=\sqrt[]{30^2+30^2} \\ r=\sqrt[]{2\cdot30^2} \\ r=30\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nu5kw6o9bd75dzj0n31q4vqei9vwt0r3br.png)
On the other hand, angle theta is given by,
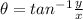
hence,
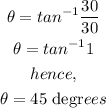
Therefore, in polar coordinates, point (30,30) is given by
![(r,\theta)=(30\sqrt[]{2},45)](https://img.qammunity.org/2023/formulas/mathematics/college/hpqf1s6izfprh5ne00ruimpd7x8twr9izz.png)
Part B
Until now, we drove 30 miles east, next 30 miles north. Now, we must drive 30 miles west and 30 miles south.
Hence, we will drive 30+30+30+30=4*30=120 miles. Therefore, the average velocity is
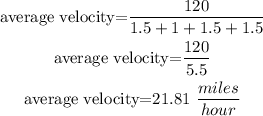
Part A. Velocity.
Velocity is a vector. In this case, we must add to vectors:
vector V1 is given by
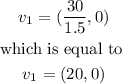
Vector V2 is given by
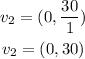
then, resultant vector velocity is