Question

Graph and label the image of the figure below after a dilation by a factor of 1/2.

Answer 1

Answer:

M' (1.5, -1), F' (2, -1), L' (0.5 -2.5), W' (2.5, -2.5)

see graph below

Step-by-step explanation:

Given:

The image of a quadrilateral on a coordinate plane

To find:

The coordinates of the new image after dilation of 1/2 have been applied to the original image.

Then graph the coordinates

First, we need to state the coordinates of the original image:

M = (3, -2)

F = (4, -2)

L = (1, -5)

W = (5, -5)

Next, we will apply a scale factor of 1/2:

`\begin{gathered} Dilation\text{ rule:} \\ (x,\text{ y\rparen}\rightarrow(kx,\text{ ky\rparen} \\ where\text{ k = scale factor} \\ \\ scale\text{ factor = 1/2} \\ M^(\prime)\text{ = \lparen}(1)/(2)(3),\text{ }(1)/(2)(-2)) \\ M^(\prime)\text{ = \lparen}(3)/(2),\text{ -1\rparen} \\ \\ F\text{ = \lparen}(1)/(2)(4),\text{ }(1)/(2)(-2)) \\ F^(\prime)\text{ = \lparen2, -1\rparen} \end{gathered}`
`\begin{gathered} L\text{ = \lparen}(1)/(2)(1),\text{ }(1)/(2)(-5)) \\ L^(\prime)\text{ = \lparen}(1)/(2),\text{ }(-5)/(2)) \\ \\ W\text{ = \lparen}(1)/(2)(5),\text{ }(1)/(2)(-5)) \\ W^(\prime)\text{ = \lparen}(5)/(2),\text{ }(-5)/(2)) \end{gathered}`

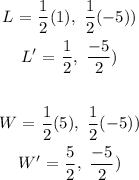
The new coordinates:

M' (3/2, -1), F' (2, -1), L' (1/2, -5/2), W' (5/2, -5/2)

M' (1.5, -1), F' (2, -1), L' (0.5 -2.5), W' (2.5, -2.5)

Plotting the coordinates: