Answer:
M' (1.5, -1), F' (2, -1), L' (0.5 -2.5), W' (2.5, -2.5)
see graph below
Step-by-step explanation:
Given:
The image of a quadrilateral on a coordinate plane
To find:
The coordinates of the new image after dilation of 1/2 have been applied to the original image.
Then graph the coordinates
First, we need to state the coordinates of the original image:
M = (3, -2)
F = (4, -2)
L = (1, -5)
W = (5, -5)
Next, we will apply a scale factor of 1/2:
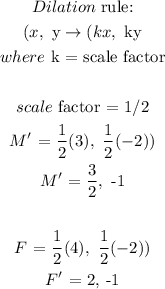
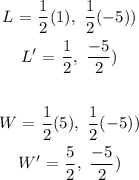
The new coordinates:
M' (3/2, -1), F' (2, -1), L' (1/2, -5/2), W' (5/2, -5/2)
M' (1.5, -1), F' (2, -1), L' (0.5 -2.5), W' (2.5, -2.5)
Plotting the coordinates: