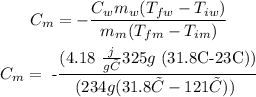Question

5. A piece of unknown metal weighing 234.0 g was heated to 121 °C, and then dropped into a beakercontaining 325 mL water at a temperature of 23 °C. The temperature of the metal and water in thebeaker stablized at a temperature of 31.8 °C. Determine the specific heat of the unknown metal.Report your answer in both J/g °C and cal/g °C.

Answer 1

To answer the question first we see the information we are given:

Mass of the metal (mm): 234 g

Mass of water (mw): 325 g, because 1 g of water equals 1ml.

Initial temperature of the metal (Tim): 121 °C

Final temperature of the metal (Tfm): 31.8 °C

Initial temperature of water (Tiw): 23 °C

Final temperature of water (Tfw): 31.8 °C

Specific heat capacity of water: 4,18 J/g °C or 1 cal/g °C

Now we know that the specific heat capacity is defined as:

`C=(Q)/(m(T_f-T_(i)))`

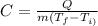
We also know that because of the law of conservation of energy all the heat that was taken from the metal (its final temperature is lower than its initial) was given to the water.

As the metal lowered its temperature we say that it lost heat and therefore Q will be a negative amount. For water it will be a positive amount.

Now we say:

`\begin{gathered} -Q_m=Q_w \\ -(C_mm_m(T_(fm)-T_(im))=(C_wm_w(T_(fw)-T_(iw)) \end{gathered}`

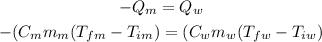
We are looking for the specific heat capacity of the metal so we rearange the equation:

`\begin{gathered} C_m=-\frac{C_wm_w(T_(fw)-T_(iw))}{_{}m_m(T_(fm)-T_(im))} \\ C_m=\text{ -}\frac{(4.18\text{ }(j)/(g\~C)325g\text{ (31.8\degree{}C-23\degree{}C))}}{(234g(31.8\~C-121\~C))\text{ }} \end{gathered}`