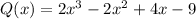The remainder theorem says that if a polynomial P(x) is divided by the binomial "x - a", then the remainder of the division is P(a). Therefore, to determine P(-2) we need to divide the polynomial P(x) by the binomial "x + 2". To do that we will use synthetic division. Using the coefficients of the polynomial.
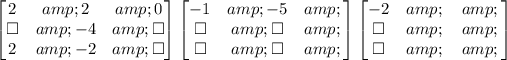
Now we take the first coefficient and multiply that by -2 and add the result to the second coefficient
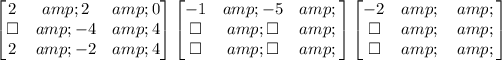
Now we multiply the result by -2 and add that to the next coefficient and so on until we get the last result which is the remainder, like this:
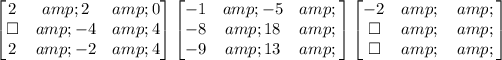
Therefore, the remainder is 13, therefore P(-2) = 13.
The quotient we find it by using the third row as coefficients of a polynomial of a grade one unit less than the original, that is: