Step 1
Given; A triangle has vertices at (-3,-3) ,(-3,2) and 1,2.
Choose from the following all the possible ways to find the length of the hypotenuse of the triangle. Then calculate the actual length. Select all correct answers; more than one answer may be correct.
Step 2
The image of the triangle is seen below.
Thus, we can find the length of the hypotenuse by;


Thus;
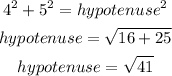
Answer;
