Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.Polygon MNOPQ is dilated by a scale factor of 0.8 with the origin as the center of dilation, resulting in the image MNOPQ. The coordinates ofpoint Mare (2, 4), and the coordinates of point Nare (3, 5).The slope of M'N' is blank

Answer 1

Given:

The points are,

`M(2,4),N(3,5)`

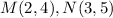
The polygon MNOPQ is dilated by a scale factor of 0.8 with the origin as the centre of dilation, resulting in the image MNOPQ.

To find:

The slope of M'N'.

Step-by-step explanation:

After the dilation by a scale factor of 0.8 with the origin,

The points become,

`\begin{gathered} M^(\prime)(0.8*2,0.8*4) \\ i.e.)\text{ }M^(\prime)(1.6,3.2) \\ N^(\prime)(0.8*3,0.8*5) \\ i.e.)\text{ }N^(\prime)(2.4,4) \end{gathered}`

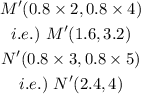
Using the slope formula,

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ Slope\text{ of M'N'}=(4-3.2)/(2.4-1.6) \\ =(0.8)/(0.8) \\ =1 \end{gathered}`

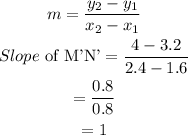
Therefore, the slope of M'N' is 1.

Final answer:

The slope of M'N' is 1.