Solution:
Given:
Round trip distance to and fro = 22.5 miles.
Total round trip time to and fro = 9 hours;
Thus; Let speed in still water = u mph
Upstream speed ( against the current ) = u - 6 mph
Downstream speed ( with the current ) = u + 6 mph
Thus, the time equation is;


Solving this quadratic, we have;
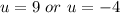
Thus, the speed is 9mph.
Thus if the boat is to serve the ferry operator’s needs, it should move at 9mph