To get the mass for these molecules, we will need to do three steps:
1 - convert from number of molecules to number of moles.
2 - calculate the molar mass for H₂O.
3 - use it to convert from number of moles to mass.
To convert from number of molecules to number of moles, we need to divide the number of molecules by the Avogadro's number:
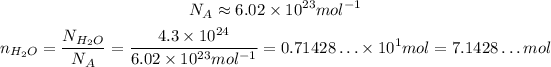
Now, to calculate the molar mass of H₂O, we need the molar masses of H and O, which we can get on a periodic table:
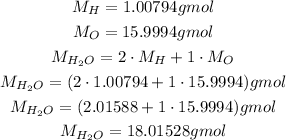
Using it, we can convert the number of moles to mass:
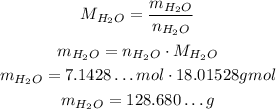
Now, the proper way of approximating this value is to maintain the same number of significant figures as the number of molecules, because we used multiplications and divisions. It has two significant figure, so we need to approximate accourdingly:
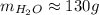
So, there is 128.680... grams or, approximately, 130 grams of water.