Let's draw a diagram to represent this situation.
To prove PM is perpendicular, first, we have to prove that angles PMQ and PMR are equal.
Notice that sides PQ and PR are equal.
Also, by midpoint definition, sides QM and RM are equal.
Additionally, PM is a common side for both triangles PMQ and PMR.
As you can observe, we have three corresponding congruent sides.
Therefore, triangles PMQ and PMR are congruent by Side-Side-Side postulate.
From the congruence between the triangles, we can deduct that angles PMQ and PMR are congruent because they are corresponding angles from the congruence.
In the image you can observe that angles PMQ and PMR are supplementary, so
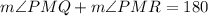
But, these angles are congruent so,
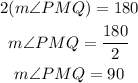
Therefore, angle PMQ is a right angle. This proves that PM is perpendicular to QR because the angles on the interception are perpendicular.