Question

Two cars leave towns 760 kilometers apart at the same time and travel toward each other, one car's rate is 10 kilometers per hour less than the other's. If they meet in 4 hours, what is the rate of the slower car? Do not do any rounding. Il kilometers per hour ?

Answer 1

v1 is the speed of car 1 (in km/h), x1 is the distance that car 1 travels (in km). Similar for car 2

One car's speed is 10 kilometers per hour less than the other's, that is,

`v_1=v_2-10`

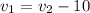
Speed is defined as distance divided by time, then

`\begin{gathered} (x_1)/(t)=(x_2)/(t)-10 \\ t\cdot(x_1)/(t)=t((x_2)/(t)-10) \\ x_1=x_2-10t \end{gathered}`

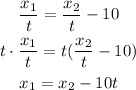
If they meet in 4 hours, then t = 4. Also, x1 + x2 must be equal to 760 km.

`\begin{gathered} x_1=x_2-10\cdot4 \\ x_1=x_2-40 \\ \\ x_1+x_2=760 \\ x_2-40+x_2=760 \\ 2x_2=760+40 \\ x_2=(800)/(2) \\ x_2=400 \\ \\ x_1=400-40\text{ = 360} \end{gathered}`

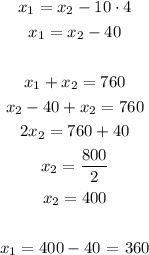
Finally, the speed of the slower car is: