We are given the expression
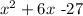
and told to factor it. First, recall that this expression looks similar to this one
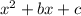
where in our case b=6 and c=-27. To check if this expression can be factored by using integers, we should look for two integers, say e and f such that the product of e and f is equal to c and the sum of e and f is equal to b. That is
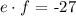
and
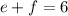
At first, notice that c=-27 is a negative number. Since -27 is the product of two integers, for it to be a negative number it must happen that at least one of them is a positive number and the other one is a negative number. Suppose that e>0 and that f<0. Now, we take a look at the factors of 27. Note that
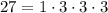
Now, in the factors of 27, we should look for a way to group them such that we get the numbers e and f we are looking for. For example, le us group it as follows
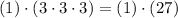
We see that 27=27*1. So for example let us take e=27 and f = -1 (remember that they should have different signs). This fulfills the criteria that e*f = -27. However e+f = 26, which is not 6. So this agrupation doesn't work.
Now let us try this
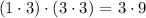
In this case we get the numbers 9 and 3. Let us take e=9 and f=-3. This fulfills that e*f=-27. Also we have that e+f = 9-3=6 which is what we wanted. So, our numbers are
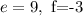
Now, to find each factor we write each factor as follows