Remainder Theorem
We want to find if
(x-11) is a factor of the polynomial:
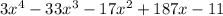
If we divide the polynomial by
(x-11)
then the remainder will be zero if it is a factor.
We find the value of the remainder by replacing:
x - 11 ⇒ x = 11
in the equation:
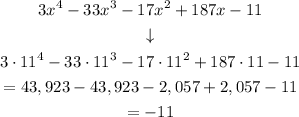
Then, the remainder if we divide the polynomial by (x - 11) is -11. This means that it cannot be a factor, since the remainder is not 0.
Answer: No, (x-11) is not a factor