Question

Is (x-11) a factor of 3x^4-33x^3-17x^2+187x-11)?

Answer 1

Remainder Theorem

We want to find if

(x-11) is a factor of the polynomial:

`3x^4-33x^3-17x^2+187x-11`

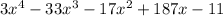
If we divide the polynomial by

(x-11)

then the remainder will be zero if it is a factor.

We find the value of the remainder by replacing:

x - 11 ⇒ x = 11

in the equation:

`\begin{gathered} 3x^4-33x^3-17x^2+187x-11 \\ \downarrow \\ 3\cdot11^4-33\cdot11^3-17\cdot11^2+187\cdot11-11 \\ =43,923-43,923-2,057+2,057-11 \\ =-11 \end{gathered}`

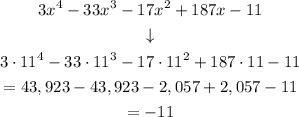
Then, the remainder if we divide the polynomial by (x - 11) is -11. This means that it cannot be a factor, since the remainder is not 0.

Answer: No, (x-11) is not a factor