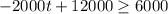We have the next points
(0,12000)=(x1,y1)
(2,8000)=(x2,y2)
First, we need to find the slope

we substitute the values
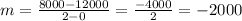
then we know that the y-intercept is 12000
where V represents the y-axis and t represents the x-axis
The equation that represents the depreciated value V as a function of t is
V=-2000t+12000
Then for the inequality, that depreciated value of V is less than 6000

Then for the inequality that describes the time t during which the depreciated values is at least half of the original, half value of the original is 12000/2=6000
t= 3 when V= 6000
therefore