Question

Given ARST with R(-1,7), S(3, -1), and T(9,2). Dete is a right triangle. of RS = of ST of RT

Answer 1

Determine the lenth of side RS with points R(-1,7) and S(3,-1).

`\begin{gathered} RS=\sqrt[]{(3+1)^2+(-1-7)^2} \\ =\sqrt[]{16+64} \\ =\sqrt[]{80} \end{gathered}`

Determine the length of side ST with points S(3,-1) and T(9,2).

`\begin{gathered} ST=\sqrt[]{(2+1)^2+(9-3)^2} \\ =\sqrt[]{9+36} \\ =\sqrt[]{45} \end{gathered}`

Determine the length of side RT with point R(-1,7) and T(9,2).

`\begin{gathered} RT=\sqrt[]{(2-7)^2+(9+1)^2} \\ =\sqrt[]{25+100} \\ =\sqrt[]{125} \end{gathered}`

Since from the above calculation it can be observed that,

`(RS)^2+(ST)^2=(RT)^2`

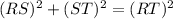
So, the triangle RST is a right angled triangle as pythagoras theorem is aplicable to the triangle RST.