Question

BASKETBALLThe average number of points a basketball team scored for three gameswas 63 points. In the first two games, they scored the same number ofpoints, which was 6 points more than they scored in the third game.Write an equation .Solve the equation to find the number of points d the team scored in each game.

Answer 1

Given:

Average number of points = 63

Number of games = 3

Score in the first two games are equal which is 6 points more than they scored in the third game.

Let's write an equation which represents this situation.

Let x represent the first two games.

Let y represent the third game.

Thus, we have:

x = 6 + y........ equation 1.

x + x + y = 63.....equation 2.

Now, let's solve both equations simultaneously using the substitution method.

Simplify the second equation:

x + x + y = 63

2x + y = 63

Substitute 6y for x in the equation:

2(6 + y) + y = 63

Apply distributive property:

2(6) + 2y + y = 63

12 + 3y = 63

3y = 63 - 12

3y = 51

Divide both sides by 3:

`\begin{gathered} (3y)/(3)=(51)/(3) \\ \\ y=17 \end{gathered}`

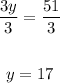
Now, substitute 17 for y in the first equation:

x = 6 + 17

x = 23

Therefore, we have the solution:

x = 23 and y = 17

Number of points scored in the first game = 23

Number of points scored in the second game = 23

Number of points scored in the third game = 17

• ANSWER:

Equations: x = 6 + y

x + x + y = 63

Number of points scored in the first game = 23

Number of points scored in the second game = 23

Number of points scored in the third game = 17