Given:
A sequence of figures is made up of triangles, using straws and dots. Shown below are the first three figures in the sequence.
We will find the relation between the number of the figure (n) and the number of straws (S) and the number of dots using the given table of part (a):
(a) Study the patterns of numbers in each row of the table below. Each row relates to one of the figures in the sequence of figures above. Some rows have not been included in the table.
As shown in the first 4 rows:
1) the number of straws is 6 times the number of figures.
2) The difference between the dots of each row = 3
We will complete the missing rows:
(i) Figure: 5, Straws (s) = 30, Dots (D) = 17
(ii) Figure = 216/6 = 36. Straws = 216, Dots = 3(36) + 2 = 110
(iii) Figure: (n), Straws = 6n, Dots = 3n + 2
Part (b), we will write an equation for S in terms of D:
First, we will write the equations in terms of (n)
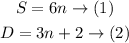
We will find (n) from equation (1) then substitute it into equation (2)
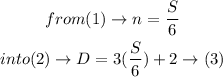
From equation (3) solve the equation for (S) to write it in terms of D
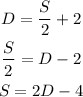
So, the answer to part (b): S = 2D - 4
Part (C):
Determine the number of dots in figure (n-1) and figure (n)
The number of dots of figure (n-1) = 3(n-1) + 2
The number of dots of figure (n) = 3n + 2
So, the total number of dots of the figures (n-1) and (n) will be as follows:
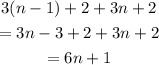
So, the answer to part (c):
The total number of dots of the figures (n-1) and (n) = 6n + 1