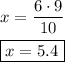Similar Polygons
In similar polygons, the ratio between every pair of corresponding side lengths is equal.
We can see the pentagons ABCDE and JKLMN are similar. Let's find the ratios between their corresponding side lengths:
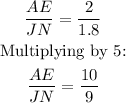
Also:
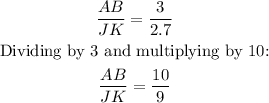
The ratios of the other side lengths BC/KL and CD/LM are also equal to 10/9.
This helps us to find the value of x because we form an equation with the known proportion as follows:

Solving for x: