The Solution:
Given the table of values below:
We are required to determine whether y varies directly with x, find the constant of variation and write out the equation that defines the relationship between x and y
Step 1:
We shall recall the formula for direct variation, which is defined as below:
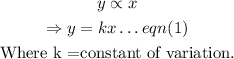
Step 2:
We shall apply the initial values of x and y, in order to find the value of k.
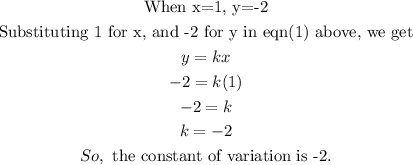
Step 3:
Substitute -2 for k in eqn(1) above.
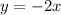
So, the equation connecting x and y is y = -2x
Step 4:
We shall check each pair of values in the table to confirm a direct variation of y with x.
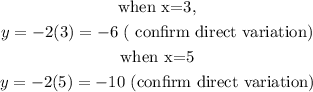
Therefore, it follows that y varies directly with x.