Answer:
(a)1/2
(b)11/24
Explanation:
Given the difference:
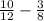
Part A
First, we estimate the difference using benchmark values.

Part B
Here, we find the actual difference.
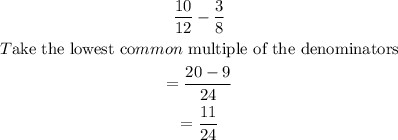
Part C
Here, the difference between the estimate and the actual value is calculated.
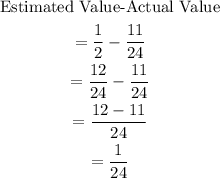
A reasonable estimate does not exceed the original numbers in the problem. Thus, the estimate for part A was reasonable.