Given information:
Two rectangles: Rectangle T and R
Since it is said on the question that the lengths of each side of Rectangle T are 4 times the length of each side of Rectangle R, we can say that Rectangle T is bigger/larger than Rectangle R.
To get the area of a rectangle, we have the following formula to use:
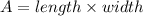
The area of Rectangle T is:
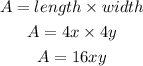
The area of Rectangle R is:
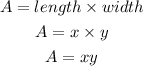
Therefore, the area of Rectangle T is 16 times larger than the area of Rectangle R.