The form of the quadratic equation is

The coordinates of its vertex are (h, k), where
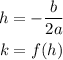
The given equation is
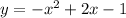
Compare it with the form above
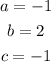
To find its x-intercepts, substitute y by 0
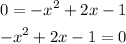
Multiply both sides by -1

Factor it into 2 factors
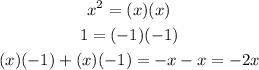
Then the factors are (x - 1) and (x - 1)
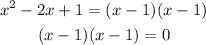
Equate the factor by 0 to find x
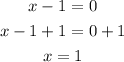
There is one x-intercept (1, 0)
To find the vertex use the rule of the vertex up
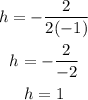
Substitute x by 1 in the equation to find k
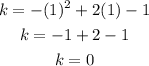
The coordinates of the vertex are (1, 0)