QUESTION A
The equation is given to be:
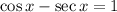
Step 1: Apply the identity:
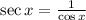
Therefore, we have:
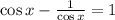
Step 2: Multiply all through by cos x:
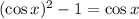
Step 3: Rewrite the equation
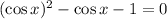
Step 4: Make the substitution for cos x = m
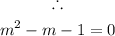
Step 5: Solve the quadratic equation using the quadratic formula
![\begin{gathered} m=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ a=1,b=-1,c=-1 \\ m=\frac{-(-1)\pm\sqrt[]{(-1)^2-4*1*(-1)}}{2*1} \\ m=\frac{1\pm\sqrt[]{1+4}}{2} \\ m=\frac{1\pm\sqrt[]{5}}{2} \\ \therefore \\ m=\frac{1+\sqrt[]{5}}{2},\frac{1-\sqrt[]{5}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/z7tbj6amc4bj8f8t5tq0tuch5du80eijt3.png)
Step 6: Substitute for m back into the solution of the quadratic equation
![\begin{gathered} \cos x=\frac{1+\sqrt[]{5}}{2} \\ or \\ \cos x=\frac{1-\sqrt[]{5}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/38b2v3rm3k4b60wawajg53kzfmf0ke0n0c.png)
Step 7: Solve for x by finding the cosine inverse of the solutions
![x=\cos ^(-1)(\frac{1+\sqrt[]{5}}{2})=\text{ undefined}]()
or
![x=\cos ^(-1)(\frac{1-\sqrt[]{5}}{2})=128.17](https://img.qammunity.org/2023/formulas/mathematics/college/w6ry9jxt8vior2oxnxgc5j87yb1wqeq09r.png)
The value of x is 128.17.
QUESTION B
The equation is:
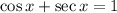
Step 1: Rewrite the equation
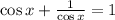
Step 2: Multiply all through by cos x
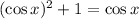
Step 3: Rearrange the equation terms
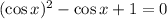
Step 4: Make the substitution for cos x = m
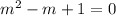
Step 5: Solve the quadratic equation
![m=\frac{1+i\sqrt[]{3}}{2},\frac{1-i\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/94cqb0n2bivvgm44relp4td6tqyytviclg.png)
Step 6: Substitute for m back into the solution of the quadratic equation
![\begin{gathered} \cos x=\frac{1+i\sqrt[]{3}}{2} \\ or \\ \cos x=\frac{1-i\sqrt[]{3}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/46a1fxeh7r85zj41lnostzyn693s0qrwww.png)
Step 7: Solve for x by finding the cosine inverse of the solutions
![\begin{gathered} x=\cos ^(-1)(\frac{1+i\sqrt[]{3}}{2})=\text{ undefined} \\ or \\ c=\cos ^(-1)(\frac{1-i\sqrt[]{3}}{2})=\text{ undefined} \end{gathered}]()
There is no solution for x.