Question

A merry-go-round at an amusement park makes 2.5 revolutions per minute. If the linear speed of a person riding on an outside horse is 3.2ft/sec, how far, in feet, is the horse from the center of the merry-go-round? Use 3.14 for pi and round to the nearest tenth.

Answer 1

In order to find the distance from the horse to the center of the merry-go-round, first let's convert the angular speed of 2.5 rev/min to rad/seconds:

`2.5(rev)/(\min)=2.5\frac{2\pi\text{ rad}}{6\text{0 sec}}=(2.5\cdot2\pi)/(60)(rad)/(s)=0.2618\text{ rad/s}`

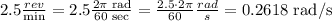
Now, in order to find the distance (which is equivalent to the radius of the circle), we can use the formula below:

`v=wr`

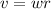
Where v is the linear speed, w is the angular speed and r is the radius.

So, for v = 3.2 and w = 0.2618, we have:

`\begin{gathered} 3.2=0.2618\cdot r \\ r=(3.2)/(0.2618) \\ r=12.22\text{ ft} \end{gathered}`

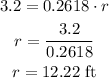
Rounding to the nearest tenth, we have a distance of 12.2 feet.