To determine which statement is correct you have to calculate the mean and standard deviation for the quiz scores of both classes.
To calculate the mean you have to add all observations and divide it by the number of observations
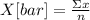
The standard deviation is the square root of the variance, to calculate the variance you have to use the following formula:
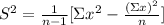
For the 2nd period scores
First, calculate the sum of the observations and the sum of the squares of the observations:
n=16
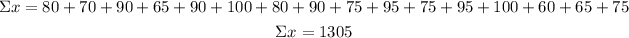
![\begin{gathered} \Sigma x^2=80^2+70^2+90^2+65^2+90^2+100^2+80^2+90^2+75^2+95^2+75^2+95^2+100^2+60^2+65^2+75^2 \\ \Sigma x^2=108975 \end{gathered}]()
Second, calculate the mean
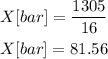
Third, calculate the variance and standard deviation
Variance
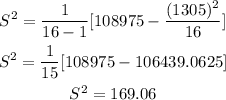
Standard deviation
![\begin{gathered} S=\sqrt[]{S^2} \\ S=\sqrt[]{169.06} \\ S=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/57hnshxv4iieaaqedaf99i1t3vhwx6e1pt.png)
For the 4th period scores
First, calculate the sum of the observations and the sum of squared of the observations
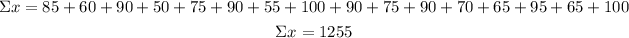
![\begin{gathered} \Sigma x^2=85^2+60^2+90^2+50^2+75^2+90^2+55^2+100^2+90^2+75^2+90^2+70^2+65^2+95^2+65^2+100^2 \\ \Sigma x^2=102375 \end{gathered}]()
Second, calculate the mean

Third, calculate the variance and standard deviation
Variance
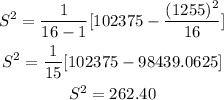
Standard deviation
![\begin{gathered} S=\sqrt[]{S^2} \\ S=\sqrt[]{262.40} \\ S=16.20 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/oowtlbhkzyvtmskhf4pw7qujjctew9hrep.png)
Now you can compare the results for both samples:
The mean score on the 2nd period is greater than the mean score on the 4th period, so on average, the students in the 2nd period performed better than the students in the 4th period.
The standard deviation of the scores of the students in the 2nd period is less than the standard deviation of the scores of the students in the 4th period, this indicates that the scores for the 2nd period are more tightly clustered about the mean than the scores for the 4th period.
With this in mind, the statements that are true regarding the data in the table are c and d