Question

1 )Solve the linear system algebraically. Write your answer as an ordered triple.

Answer 1

Given

Linear equations

`\begin{gathered} x-3y+3z=-4...............1 \\ 2x+3y-z=15.......................2 \\ 4x-3y-z=19..................3 \end{gathered}`

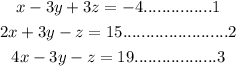
Find

Value of x , y and z

Step-by-step explanation

from equation 1 , find the value of x in terms of y and z , and then put in equation 2 and 3 .

`\begin{gathered} x-3y+3z=-4 \\ x=-4+3y-3z \end{gathered}`

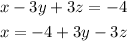
now put in equation 2 and 3

`\begin{gathered} 2(3y-3z-4)+3y-z=15 \\ 9y-3z=23.........(4) \end{gathered}`

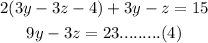
and

`\begin{gathered} 4(3y-3z-4)-3y-z=19 \\ 9y-13z=35..................(5) \end{gathered}`

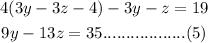
now subtract equation 4 and 5

`\begin{gathered} 9y-7z-9y+13z=23-35 \\ 6z=-12 \\ z=-2 \end{gathered}`

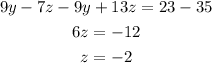
now put value of z in equation 4.

`\begin{gathered} 9y-7(-2)=23 \\ 9y+14=23 \\ 9y=9 \\ y=1 \end{gathered}`

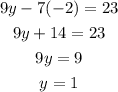
now put value of y ana z in equation 1.

`\begin{gathered} x-3(1)+3(-2)=-4 \\ x-3-6=-4 \\ x=5 \end{gathered}`

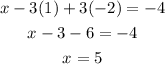
Final Answer

Therefore , the ordered triple is {5 , 1 , -2}