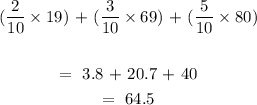Question

Professor Walter informed her students of their scores on the midterm exam. Score Number of students 19 2 69 3 80 5 X is the score that a randomly chosen student scored. What is the expected value of X? Write your answer as a decimal.

Answer 1

The expected value of x is 64.5

Here, we want to get the value of x, which is the expected a score a randomly chosen student scores

What we have to do here is to set up a probability distribution, with the number of students as the frequencies f and the scores x

We are to base the probability on the number of students and not the scores

The mean of the probability distribution will represent the expected value of x

The total number of students is (2 + 3 + 5) = 10

We have the calculation of the mean of the probability distribution as follows;

`\begin{gathered} ((2)/(10)*19)\text{ + (}(3)/(10)*69)\text{ + (}(5)/(10)*80) \\ \\ =\text{ 3.8 + 20.7 + 40} \\ =\text{ 64.5} \end{gathered}`